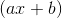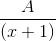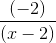Dalam matematika, polinomial atau suku banyak adalah pernyataan matematika yang melibatkan jumlahan perkalian pangkat dalam satu atau lebih variabel dengan koefisien. Sebuah polinomial dalam satu variabel dengan koefisien konstan memiliki bentuk seperti berikut:
Pangkat tertinggi pada suatu polinomial menunjukkan orde atau derajat dari polinomial tersebut.
FUNGSI POLINOMIAL
Secara umum,bentuk fungsi polinomial adalah sebagai berikut
P(X) =
Nilai Fungsi Polinomial
Jika suatu polinom dilambangkan dengan p(x), maka nilai polinom untuk x=2 adalah p(2).
jika
maka
Polinomial Identik
Dua suku banyak (polinomial) dikatakan sama (identik) apabila kedua poinom tersebut memiliki derajat dan koefisien-koefisien suku sejenis juga yang sama. Misalnya :
Bandingkan koefisien
Bandingkan koefisien
Sifat Operasi Aljabar pada Polinomial
Dalam polinomial berlaku penjumlahan, pengurangan dan perkalian seperti halnya aljabar. misalnya :
Diketahui P(x) = (5x³+3x²-6) dan F(x) = (x²-4x+2). Tentukanlah
P(x) – F(x)!
maka,
P(x) - F(x) = ( 5x³ + 3x² - 6) - ( x² - 4x + 2 )
= 5x³ + 2x² + 4x - 8
Diketahui
P(x)=(3x²+4x) dan F(x)=(x³+5x-2). Tentukanlah P(x).F(x) !
P(x) . F(x) = (3x²+4x)(x³+5x-2)
= 3x²(x³+5x-2)+4x(x³+5x-2)
= 3x²(x³+5x-2)+4x(x³+5x-2)
= (3x⁵+15x³-6x²)+(4x⁴+20x²-8x)
= 3x⁵+4x⁴+15x³+14x-8x
Faktor Dari Suatu Polinomial
Kita dapat mengetahui apakah suatu akar merupakan akar dari suatu poinom dengan cara mensstubtitusikan akar tersebut kedalam polinom.Jika hasilnya = 0 maka bilangan tersebuat adalah akar polinom. Misalnya :
Diketahui polinom =&space;x^{3}-6x^{2}-x+30 "P(x)= x^{3}-6x^{2}-x+30")
. Apakah x=3 merupakan akar dari polinom tersebut ?
untuk x=3 maka,=&space;3^{3}-6.3^{2}-3+30 "P(3)= 3^{3}-6.3^{2}-3+30")
karena p(3)= 0 maka x=3 adalah akar polinom p(x)
Kita juga dapat mengetahui apakah suatu faktor merupakan faktor dari suatu polinom dengan cara pembagian, horner dan substitusi. Jika sisa pembagian, horner dan subtitusi = 0 maka, itu merupakan faktor polinom tersebut.
Diketahui polinom. Apakah x+2 merupakan faktor dari polinom tersebut ?
misalkan x+2=0 , maka x=-2
P(-2)=(-2)3–6.( -2 )2–( -2 )+30
= 0
karena p(-2)=0, maka x+2 adalah faktor dari P(x).
P(x)= x3 – 6x2 – x + 30
jadi, nilai f(–3)= –35.
untuk x=3 maka,
karena p(3)= 0 maka x=3 adalah akar polinom p(x)
Kita juga dapat mengetahui apakah suatu faktor merupakan faktor dari suatu polinom dengan cara pembagian, horner dan substitusi. Jika sisa pembagian, horner dan subtitusi = 0 maka, itu merupakan faktor polinom tersebut.
Diketahui polinom
misalkan x+2=0 , maka x=-2
P(-2)=(-2)3–6.( -2 )2–( -2 )+30
= 0
karena p(-2)=0, maka x+2 adalah faktor dari P(x).
P(x)= x3 – 6x2 – x + 30
= (x+2)(x-3)(x-5)
NILAI POLINOMIAL
Untuk permasalahan ini kita dapat menyelesaikannya dengan cara horner. misalnya :
Diketahui f(x)=x5+2x4–3x³–x²+7x–5. nilai f(–3) adalah ?
PEMBAGIAN POLINOMIAL
Pembagian pada polnomial dapat dilakukan dengan 2 metode yaitu, pembagian kebawah dan horner. misalnya :
1. Pembagian Biasa
1. Pembagian Biasa
F(x) = 2x3 – 3x2 + x + 5 dibagi dengan P(x) = 2x2 – x – 1
Sehingga hasil baginya: H(X) = x – 1, sisanya S(x) = x + 4
2. Cara Horner
Jika(2x3 – 5x2 + 4x + 3)dibagi dengan (x – 3) !
hasil bagi = 2x2 + x + 7
sisa pembagian = 24
TEOREMA SISA
bentuk suku banyak pada pembagian suku banyak dapat dinyatakan dalam bentuk persamaan umum berikut.
![\[ f(x) = p(x) \cdot H(x) + S(x) \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-cbb230f6351f5a60b371078cdba5c664_l3.png "Rendered by QuickLaTeX.com")
Keterangan:
f(x) = suku banyak
p(x) = pembagi suku banyak
H(x) = hasil bagi suku banyak
S(x) = sisa suku banyak
f(x) = suku banyak
p(x) = pembagi suku banyak
H(x) = hasil bagi suku banyak
S(x) = sisa suku banyak
Pada pembagian polinomial , jika pembagi bukanlah faktor dari polinomial tersebut maka pembagian tersebut akan menghasilkan H(x) dan menyisakan S(x). Misalnya :
Diketahui f(x) = x5 + 2x4 – 3x³ – x² + 7x – 5.
- Tentukan hasil bagi dan sisa f(x) jika dibagi dengan x + 3.
- Gunakan Teorema Sisa untuk menentukan f(–3).
Pembahasan
- Karena x + 3 = x – (–3), maka kita dapat melakukan pembagian suku banyak seperti berikut.
Hasil baginya adalah x4 – x³ – x + 10 dan sisanya adalah –35. - Berdasarkan Teorema Sisa, f(–3) merupakan sisa pembagian f(x) oleh x – (–3) = x+ 3. Dari bagian (1) kita telah menemukan sisanya adalah –35. Sehingga f(–3) = –35.
TEOREMA FAKTOR
Pada Teorema Faktor, misalkan nilai
polinomial atau suku banyak P(k) = 0, maka suku banyak P(x)
bersisa 0 apabila dibagi dengan x – k.
Dengan demikian, (x – k) dikatakan
sebagai faktor dari P(x).
Kesimpulan :
1. Jika (x – k) merupakan faktor
dari P(x), maka P(k) = 0.
2. Jika P(k) = 0, maka (x – k) merupakan faktor dari P(x).
Contohnya,
Buktikanlah bahwa (x + 3) adalah faktor dari x3 + x2 – 9x – 9.
Jawab
:
Jika
(x + 3) adalah faktor dari f(x) = x3 + x2 – 9x – 9, maka f(–3) = 0
f(-3)
= x3 + x2 – 9x – 9
f(-3)
= (-3)3 + (-3)2 – 9(-3) – 9
f(-3)
= -27 + 9 + 27 – 9
f(-3)
= 0
Maka,
terbukti bahwa (x + 3) adalah faktor dari x3 + x2 – 9x – 9
PERSAMAAN POLINOMIAL
1. Menyelesaikan Persamaan
Polinomial
Prinsipi yang digunakan untuk
persamaan polinomial yaitu sebagai berikut :
anxn + an-1xn-1 + an-2xn-2 + … + a2x2 + a1x + a0
= 0
Contohnya,
Tentukan himpunan penyelesaian
persamaan x3 – 4x2 + x + 6 = 0
Jawab :
Koefisien x3 = 1, faktor
: 1
Konstanta = 6, faktor ±1, ±2, ±3,
dan ±6
Tentukan sisa pembagian 0 dengan x
= -1 (dihornerkan)
Sehingga bentuk persamaan tersebut menjadi
(x + 1)(x2 – 5x + 6)= 0
(x + 1)(x – 2) (x – 3)= 0
X = -1 atau x = 2 atau x = 3
Jadi, himpunan penyelesainnya adalah {-1, 2, 3}
2. Hubungan Akar-Akar Polinomial
dengan Koefisien-Koefisien Suku
·
Polinomial berderajat 2 (ax2
+ bx + c)
X1 + X2 = (-b)/a
X1 . X2 = c/a
·
Polinomial berderajat 3 (ax3
+ bx2 + cx
+ d)
X1 + X2 + X3 = (-b)/a
X1 . X2
. X3 = (-d)/a
·
Polinomial berderajat 4 (ax4
+ bx3 + cx2
+ dx + e)
X1 + X2 + X3 + X4 = (-b)/a
X1 . X2
. X3 . X4 = e/a
Contohnya,
Jika persamaan 2x3 + px2 - 18x + 8 = 0
memiliki dua akar yang saling berlebalikan, tentukan nilai p.
Jawab :
Misalkan akar-akar polinom
2x3 + px2 - 18x + 8 = 0 adalah x1, x2,
dan x3. Dua akarnya berkebalikan,
x1 = 1/x2
x1. x2 = 1
Gunakan rumus perkalian akar-akar
X1 . X2
. X3 = (-d)/a
1 . X3 = 
X3 = -4
Maka,
2(-4)3 + p(-4)2 – 18(-4) + 8 = 0
= -128 + 16p + 72 + 8 = 0
= 16p = 48
p = 3
FUNGSI PECAHAN SEBAGIAN
Pecahan dapat dinyatakan sebagai berikut :
= 
= 1 + 
Sedangkan pecahan dapat
dinyatakan sebagai berikut :
= 
= 
+ 
= 
+ 
Bandingkan derajat pembilang ruas kanan dengan derajat penyebut
ruas kiri pada dua pecahan di atas:
“Derajat pembilang sekurang-kurangnya satu kurangnya dari
derajat penyebut sebelumnya”.
Untuk setiap faktor
linear 
pada penyebut, terdapat satu pecahan dalam
bentuk 
di mana A konstanta.
pada penyebut, terdapat satu pecahan dalam
bentuk 
di mana A konstanta.
Misalnya :
= 
=
+ 
+ 
Contohnya,
Tentukan nilai A dan B pada
= 
+ 
= 
+ 
Jawab :
= 
= 
… (*)
… (*)
Untuk koefisien x1 : 1 = A + B … (1)
Konstanta : -12 = 3A – 2B … (2)
Dari (1) dan (2)diperoleh A = -2 dan B = 3.
Jadi,
= 
+ 
= 
+ 
MASALAH YANG MELIBATKAN POLINOMIAL
Contoh soal:
Sebuah perusahaan sepatu mempunyai persediaan bahan baku kulit yang memenuhi persamaan: f(x)=X3-4x2+5x , di mana x dalam meter.
Apabila bahan baku untuk sebuah sepatu
memenuhi persamaan(x-2), tentukan:
a)jumlah sepatu yang
dapat diproduksi, dan
b) sisa bahan baku setelah
produksi.
Jawab :
a) 
Jumlah sepatu yang
dapat diproduksi merupakan hasil bagi
Jumlah sepatu yang
dapat diproduksi merupakan hasil bagi
persediaan bahan baku dibagi bahan baku.
Dengan menggunakan cara
Horner, diperoleh hasil :
b. Dari cara Horner pada soal
(a)diperoleh sisa bahan baku setelah diproduksi adalah 2 meter bahan baku
kulit.
